素数とは無限に続く数である

「おいしいケーキがあるから、暇やったら、うちに来(こ)ーへん？(来ない？)」
素数の話題が乱れ飛んだ女子会から1週間後、ともはまゆの家に招かれた。
特に予定もないし、タダでおいしいケーキを食べられるのなら…と“お呼ばれ”に預かることにしたのだが…

まゆ：いらっしゃ〜い。待ってたでぇ

とも：大歓迎やなｗ

まゆ：ささ、入って入って。おいしい紅茶もあるでぇ

えりか：こんにちは

とも：こ、こんにちは

まゆ：この子は私の姪っ子で、えりか。おいしいケーキの話したら「私も混ぜて」って言うもんやから…

とも：別にかまへんで。えりかちゃん、はじめまして〜

まゆ：この茶髪のおばちゃんは、私の助手のとも(※1)

とも：私がおばさんやったら、あんたもおばさんやん。それに助手ってなんやねんな

まゆ：まぁ、えりかから見て、私は叔母さんに違いないけどな

とも：そぉ来たか。完全にアウェーや

まゆ：ところで助手のとも姐さん。おいしいケーキ食べさせたるから、えりかの夏休みの宿題、手伝だってんか？

とも：はぁ？

まゆ：えりかは、すごいんやでぇ。私の素数の話を聞いて、夏休みの自由研究に「素数」を選んだんやで

とも：まゆは家でも素数の話しかせえへんのんか？

まゆ：ともが振ってきたアイスクリームの話が私の胸の中に眠っていた素数魂を呼び起こしたんやな。きっと

とも：あのアイスクリームの話って、話の成り行きから軽くネタを振っただけやで。まさか「素数やから」って返してくるとは思わんかったわ(※2)

まゆ：そこで、えりかの夏休みの自由研究として、素数が無限にある証明をしたいと思う

とも：証明も何も、数が無限にあるんやから、素数も無限にあるもんと違うの？

まゆ：えりか、今のともの発言からメモ！

えりか：はいっ。数が無限にあるから素数も無限にあるのでは…φ(..)メモメモ

とも：ええええぇ？！

まゆ：今のともの発言は、序章としては最高やｗ

とも：私って、褒められてるんか？

まゆ：普通の人は、たいてい、そぉ思うよねｗ

とも：一転、馬鹿にされたような…

まゆ：でも、素数が無限にあるのは簡単に証明できるんやなぁ。これを「ユークリッドの定理」って言うねん(※3)

えりか：ユークリッドの定理っと…φ(..)メモメモ

まゆ：素数が無限にあることを今から証明するんやけど…あ、でもええわ。あとで、ともおばさんがおもしろおかしくまとめてくれるから

とも：あんたに、おばさんって言われる筋合いはない。それに私は宿題代行業者やないでｗ

まゆ：それで、今、発見されている最大の素数を「P」としよう。「素数は無限にある」という話に矛盾するようやけど

えりか：はい

まゆ：それで最小の素数である「2」から順番に、最大の素数と仮定した「P」まで、すべての素数を掛け算するんや。とも、そこにパソコンあるから、Excelで計算して！

とも：できるかっ！

まゆ：よぉそれでExcelスペシャリストって自慢できるなぁ

とも：別に自慢はしてない。そもそも「P」って、いくつやねんなｗ　この前、現在発見されている最大の素数は1700万桁を超えるとか言ってなかったか？(※2015年9月現在)

まゆ：じゃあ、2×3×5×7×…としていって「P」まで掛け算したことにしよっか

とも：とんでもない数が出来そうやな

まゆ：でもな、逆に考えると、その数は「2」から「P」まで順番に割っていくと、すべての素数で割り切れる数になるやろ

とも：掛け算した合計やから、掛けた素数で割り切れるなぁ

まゆ：つまり、素因数分解できるから、素数ではないんやな。ここで問題。その数に1を足したら、どうなる？

とも：どうなるって、どうなるのん

まゆ：えりか、その数を素因数分解できると思う？

えりか：わからないです…

まゆ：うん、わからんよね。じゃあ、順番にやってみよか。助手のとも姐さん

とも：ちょい待ち！この話、何年かかるねんｗ

まゆ：心配せんでも来年の夏休みが終わる頃には終わらせてみせる！（ガッツポーズ）

とも：来年なんかいｗ　今年の宿題には間に合わんやんｗ

えりか：（この人らに宿題手伝ってもらって、大丈夫やろか）

まゆ：じゃあ、考え方を変えよう。今知られている最大の素数は「3」と仮定しよっか。で、知られている最大の素数「3」までの素数をすべて掛けて、その数に1を足してみる。

えりか：2×3＋1…だから7？

まゆ：ほらほらほら、7って素数やん。「3」が最大の素数の世界に「3」を超える素数が誕生した瞬間や！

とも：ほぉ。なるほど

まゆ：じゃあ、今、「13」が最大の素数だったとする。で、2から13までの素数を掛け合わせた数に1を足してみよっか。とも

とも：え、私？！

まゆ：暗算でせぇとは言わん。得意のExcel使ってええでｗ

とも：パソコン起動してExcel起動する時間を考えれば、スマホの計算機で計算するわ。えっと「2×3×5×7×11×13＋1」やから30,031やな

まゆ：30,031って、素数やと思う？

とも：素数と違うのん？素数をかけた数に1を足したんやから、素因数分解は、できなさそうやで

まゆ：では、この前、ともが作った素数判定Excelで調べてみよう！

とも：結局、パソコン起動してExcel立ち上げるんかｗ

まゆ：これが、とも姐さん自慢の素数判定マシーン！

とも：マシーンって、ただのExcelファイルやんか。それも数式が1行しか入ってないｗ(※4)

まゆ：えりか、A1のマスに、30,031を入れてみよっか

とも：前も言ったけど「マス」やのぉて「セル」や

えりか：（カタカタ）。「30031 は素数と違うわ！残念やなぁ」

とも：え、素数と違うの？

まゆ：素因数分解してみよっか。とものExcelが、こわれとぉ可能性もあるし。Excelで素因数分解してｗ

とも：すごい無茶ぶりやな。とりあえず、30031を素数で順番に割ってみよっか（カタカタ）

えりか：ともさんのキー裁き、すごいです！

とも：なんやったら、今から、お姉さんが、えりかちゃんにExcel教えよっか？　素数よりは役立つで

まゆ：今は夏休みの宿題片付けよう！

えりか：はい…

とも：59で割れたで。「素数を掛け合わせた数に+1した数は素数」という前提が崩れたで。まゆ！

まゆ：そんな前提を設定した覚えはないでｗ

とも：あれ、そうやったっけ？

まゆ：唯一の前提は「13が最大の素数の世界」というだけ。この式の答えが素因数分解できたからといって慌てることはありません！(キッパリ)

とも：あ、そっか。13が最大の素数の世界やから、少なくとも「59」は…

まゆ：ここから先はえりか、答えてみよっか

えりか：13が最大の素数の世界に、13よりも大きな素数が発見されたということですか?

まゆ：つまりそういうこと。素因数分解ができたとしても、前提の最大の素数より、より大きな素数ができるんよね。13が最大の素数の世界の記録が塗り替えられました。この世界の最大の素数は？

えりか：59…？

まゆ：そぉ思うやろ。素因数分解できるということは、59ではなく…相方の「509」も素数と思わん？

えりか：あっ

まゆ：素数判定Excelに509を入れてみよっか

えりか：「509は素数やん！」

とも：なんか、だまされてるみたいやわ

まゆ：今回は59の相方の509もたまたま素数やったけど、相方が合成数の場合もあるから要注意！

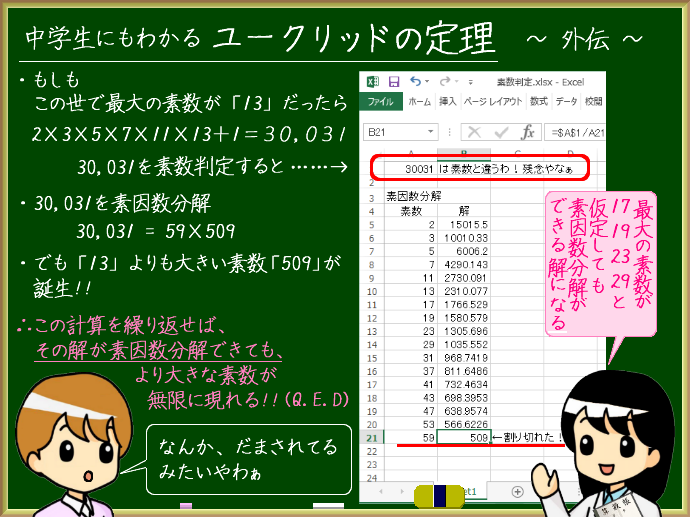
まゆ：まとめると…
【数式】この世界で最大の素数「P」までの素数を2から順番に掛けていき、その答えに1を足す
【解1】解が素数だった場合は、もとの「P」よりも大きな素数である。
【解2】解が素数で割り切れた(素因数分解できた)としても、割った素数は「P」よりも大きな素数である。
【結論】どっちに転んでも、この式で計算を続ける限り、もとの素数「P」より大きな素数が誕生する。
∴素数は無限に存在する。
…わけやね

とも：おお、凄いな！こんな方法で、素数が無限に続くことを証明できるなんて。じゃあ、証明が終わったことやし、ケーキにしよう！な、えりかちゃん！

えりか：はい！

まゆ：あんたら、素数より食い気やな

とも：それ、普通やから！

♥ 脚注 ♥

※1　茶髪
　とも曰く「茶髪って言わんといて！　イラストではデフォルメされてるけど、極めて黒髪に近い茶髪やで」

※2　「第1話　素数とは夏の数である」を参考のこと。

※3　エウクレイデス(ユークリッド)
　紀元前3世紀のギリシャの数学者。数学史上最高の著作といわれる『原論(ユークリッド原論)』の著者として知られる。「ユークリッドの定理」もこの『原論』に登場する。
　ちなみに『原論』に「エウクレイデス」の署名があることから「エウクレイデス」の著書とされているが、「エウクレイデス」にはギリシャ語で「よき栄光」という意味もあることから、「エウクレイデス」という数学者は実在しなかったという説もある。

※4　「第4話　素数とはExcelで見つけられる数である」を参考のこと。