素数とはExcelで見つけられる数である

まゆ：そろそろ、ともの本気を見せてもらおうかな

とも：本気って何？

まゆ：あんたのExcelスキルを総動員して、ずばり素数を見つけるねん。ある数を入力したら、それが素数かどうか判定するだけでええんやけど…

とも：はぁ？　前に、1つの式ですべての素数を見つける方法はないって言ってなかったっけ？

まゆ：ないけど、パソコン使ったらなんとかなるんとちゃうの？　Excelって、そぉいうもんやろ？

とも：Excelは素数探すためのソフトやないでｗ　とはいえ、複数の式で見つけられるんやったら、できなくはないかも

まゆ：そやろ

とも：ちょっと待った！その前に、私、素数を見つける式とか、知らんやん

まゆ：簡単簡単。ある数を素数判定したかったら、2から、その数までの整数で割り算を繰り返せばええねん。割り切れなかったら素数

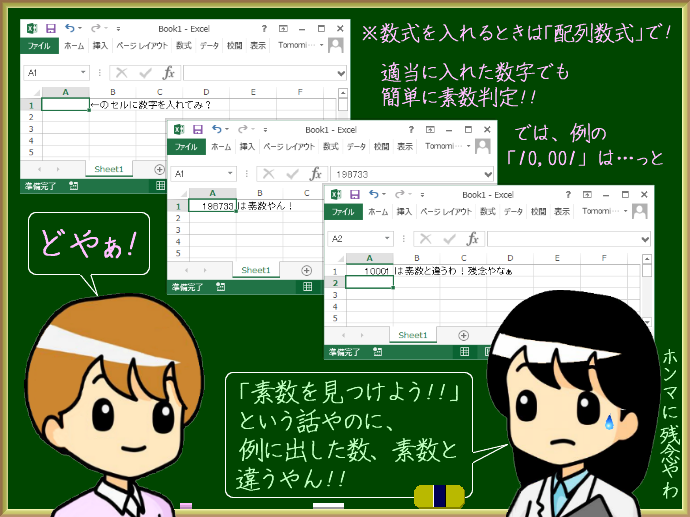
とも：いやいやいや。ざっくりしすぎやｗ　「10,000」とか入力されたら10,000回も割り算を繰り返すんか？

まゆ：10,000はExcel使うまでもなく素数やないから大丈夫

とも：ごめん、私が悪かったｗ　じゃあ「10,001」が入力されたら、10,001回も割り算するんか？パソコンが非力やったら、Excel死ぬわ

まゆ：実際は、そんなに計算せぇへんで。最初の2で割る計算やけど、2で割れたら、その時点で素数ではないので終わり

とも：10,001は、私でも、一目見ただけで、2で割れないことぐらいわかるわ

まゆ：2で割れなくても大丈夫。2で割れないとわかった時点で「偶数で割れない」ので、偶数での割り算はしなくてもええで

とも：半分に減ったと言っても約5000回は計算せんといかんやん

まゆ：裏技があるんよ。裏技がｗ

話が長くなるので、まゆの話をまとめると、素数は基本的に次の手順で判定できる。

• ある数(以下nとする)が素数であるかを判定する方法として、2からnまでの整数で順番に割り算を繰り返す
• 2で割り切れると偶数。ただし2は素数なので、2以外の偶数の場合、nは素数ではない
• 2で割り切れなかった場合、 nは奇数なので、nまでの奇数で割り算を繰り返し、どれかの数で割り切れれば素数ではない
• nと1以外の奇数で割り切れなければ、素数(※1)

まゆ：実はnを素数判定したかったら√nまでの整数で割り算を繰り返せばええねん

とも：る、ルート?

まゆ：nが合成数やったら、nの約数同士を掛け算するとnになるペアが何種類かできるんやけど、そのペアを分けてるのが、実はnの平方根

• たとえば、nが72であった場合、その約数は1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
• この約数を掛け合わせて72 になるペアは…1×72, 2×36, 3×24, 4×18, 6×12, 8×9 が見つかる
• しかし9以上の約数同士を掛けて72にすることはできない。見方を変えると72は8までの数で割り切れる

まゆ：つまり、8と9の間に、素数判定の秘密が隠されている…と思わへん？

とも：どういうこと？

まゆ：72を例にすると、√72は少数で8.4852…になるんで、8と9の間に√72があるやろ。72は合成数なので√72までの整数で割り切れるけど、nが√nまでの整数で割り切れなければ、nは素数ということになるやん。

とも：なるほど。10,001を素数かどうか判定するには√10001までの整数。つまり100までの奇数で割り算を繰り返せばええんやな。

まゆ：厳密に言うならば100までの素数で割り算を繰り返せばええんやけど、そのやり方では、100までの数の素数判定もせんとあかんので、平方根までの全ての奇数での割り算が現実的やろなぁ。これぐらいやったら、Excelでできるんと違うん?

とも：できそうな気がするなぁ。どういう数式になるんか考えてみるわ

【コピペ方法】

• Excelの「B1」セルに上記の数式をコピペ。
• コピペ後、[Shift]+[Ctrl]+[Enter]キーで、数式を確定してください。
  ※この数式は、同じ計算を指定の範囲で繰り返し演算する「配列数式」のため、コピペ後、[Enter]キーだけで確定すると、うまく機能しません

【使い方】

• A1セルに好きな数を入れて、[Enter]キーを押すと、素数か、そうでないかを判定します。
• Excel2013以降であれば「1,099,511,627,776」までの数の素数判定ができます。マイナンバーの素数判定も余裕です。
• Googleスプレッドシートでも使うことができます。Googleドライブに置くと、いつでもどこでも素数判定ができますね(誰得)。
  ※Googleスプレッドシートでは「268,435,455」までしか素数判定ができません。

【JavaScript版素数判定ツール】

• 処理は端末に依存するため、スマートフォン等では利用状況によってフリーズする場合もあります。

まゆ：で、10,001は素数なん?

とも：違うみたいよ(※4)

まゆ：ずばり素数を見つけようという話やのに、素数でない数を例にするなんて…。これまでの説明が台無しやん

とも：え、それって、私が悪いの?

♥ 脚注 ♥

※1　エラトステネスのふるい
　エラトステネス(BC276〜BC195)はギリシャの数学者。ある数が素数かどうか知りたい場合、その数を2から整数で順番に割り、最後まで割り切れなかった場合は素数であることを発見した。
　これを応用して、100までの素数をすべて見つける場合、1〜100までの数のうち、まず1を消し、次に2〜10までの数で順番に割り、2,3,5,7以外の数で割り切れた数を消して、残った数が100までの素数となる。これを「エラトステネスのふるい」という。
　つまり100までの数は、100までの割り算をしなくても、10までの数を順番に割ることで判断できる。勘のいい読者は気づいたと思うが、100を分解すると「10×10」。つまり10は100の平方根なので、10までの数を割ることで100までの素数を見つけることができるのだ。本文中の解説も基本は同じ原理である。

※2　割り算の回数について
　本稿では解説を簡単にするため、素数を判定する数(以下 n )の半分までの数を計算するとしているが、厳密には下記の段階を踏むため、割り算を繰り返す回数は、さらに減る。
・2で割り切れなかった場合
　次の計算(3で割るとき)は n × 1/3 までの奇数(正確には素数)まで割り算を繰り返す
・3で割り切れなかった場合
　次の計算(5で割るとき)は n × 1/5 までの奇数(正確には素数)まで割り算を繰り返す
・5で割り切れなかった場合
　次の計算(7で割るとき)は n × 1/7 までの奇数(正確には素数)まで割り算を繰り返す
これを繰り返して、割る数が、√ nを超えた時点で割り切れなければ、 n は素数である。

※3　参考
Test if a Number is Prime using a Formula in Microsoft Excel
　[A1]セルに入力された数字を、最小の素数である2〜[A1]セルの平方根までにある整数(処理上、小数点以下を切り上げている)で割り算を繰り返し、最後まで余りがあると素数と判定しています。ただし、これだけでは2を素数とみなさないため、2が入力されたときだけ、計算をせずに素数と判定しています。

※4　10,001が素数でない理由
素因数分解すると… 10,001 = 73 × 137
∴素数ではない (Q.E.D)