素数とは安全も違法もある数である

まゆ：初めてハロウィンパーティっていうのに出たけど、めっちゃ楽しかったわ!

とも：そやろーって、さっきから聞こうと思ってたんやけど、それ、なんの仮装なん？

まゆ：素数姫に決まっとぉやん。重要アイテムの算数帳も持っとぉからわかるやろ

とも：それ、普段着やん

まゆ：普段着っていうな！メドゥーサに言われたくないわ。あ、そうや。私の車で家まで送ろっか?(※1)

とも：車?　あんた、ビール飲んでたやん。車運転して帰ったらアカンやん

まゆ：あれ、ノンアルコールビールやで。車で来てるのに、お酒なんか飲むわけないやん

とも：そういえば、まゆが運転する車って初めて乗るけど、運転、大丈夫か？

まゆ：自慢やないけど、私、ゴールド免許やで

とも：じゃあ、安全運転、頼むで！

まゆ：任しといて！　あ！そうや！

とも：何？忘れ物でもしたん？

まゆ：安全と言えば「安全素数」って知っとぉ?

とも：え？あ、あの、私、やっぱり電車で帰るわ

まゆ：(アクセルを踏む)　もう遅い！車動いとぉし

とも：あんた、今、アクセル踏んだやろ！

まゆ：アクセルを踏まんと車、動かんやん

とも：車の機能のことを言うてるんやないっ！

まゆ：で、素数には「安全素数」っていうのがあるねん

とも：へぇ。それはよかったなぁ。じゃあ、私、寝とくから、着いたら起こしてや

まゆ：1人で寝るな！私も眠くなるやろ！家まで送ったげるんやから、私の話に付き合いぃな

とも：しゃあないなぁ。じゃあ、その安全素数って、何が安全なん?

まゆ：ある素数をpとすると、その素数pを2倍して1を足してできた素数(2p+1)のことを安全素数っていうねん。なぜ、その素数が安全かというと、暗号が解かれにくい素数やねん

とも：そぉいえば、前に素数はネット上の暗号技術は素因数分解が解かれにくいことによって成り立ってるっていう話をしてたなぁ(※2)

まゆ：そう、暗号化で使われる素因数分解っていうのは、ある巨大な数字を答えとする2つの素数の掛け算を見つけること。それが見つかると暗号が解かれるっていうことやね。2個の素数のうち1個だけでも素数が見つかってしまったら、2個目を見つけることは簡単

とも：つまり、1個の素数がわかったら、元の巨大な整数を、その素数で割れば、必然的に2個目の素数が見つかるってことやろ

まゆ：うん。そういうことなんで、素数自体も暴かれにくい素数にしておく必要がある。つまり数学的に暴かれにくい素数が安全素数っていうわけやね

とも：ん?　数学的に暴かれにくいっていうのが引っかかるなぁ。pが2の場合、まゆの話では2×2+1=5 が安全素数になるやん

まゆ：確かに5も安全素数やけど、どこの世界でそんな小さい数字を暗号で使うねんな。そもそも安全素数が安全であるためには、pも巨大な数にしておく必要があるねん。なぜかというと、まずpを2倍にした数字は2とpで割り算できるけど、これに1を足すと、それが素数なのかどうかも判定が難しくなるねん

とも：2p+1が素数でない場合もあるんや

まゆ：一番簡単な例やと、pが7やったら、2×7+1=15で素数と違うやろ

とも：ほんまや。私はてっきり、2p+1は全て素数になると思ってたわ。それやったら、逆にそこから簡単に暗号化の素数を簡単に見つけられると思ったけど、そもそも、その数が素数かどうかも判定せんとアカンわけか。うまいことできとぉなぁ

まゆ：ほんまやったら、もっと難しい理論があるけど、興味があったら先生にでも聞いて

とも：先生って誰やねん(笑)

まゆ：ちなみに2p+1が素数やったときのpを「ソフィー･ジェルマン素数」っていうねん

とも：名前からしてエレガントな響きやん。ソフィーっていうことは、名前の主は女性やな(※3)

まゆ：ご想像通り女性。それで天才数学者ガウスさんのメル友やねん。って、さっきまで眠そうにしてたのに、あんたの目ぇ輝いてるで(笑)

とも：ガウスも隅に置けんなぁ。そぉやって美しい女性を…

まゆ：妄想を膨らませすぎや(笑)。実はソフィーさんは男性を装ってガウスさんと手紙のやりとりをやってたんや

とも：え！ガウスって男色家やったん？そんな面白い素数の話があるんやったら、もっと早く教えてぇな

まゆ：あんたは腐女子か！そういうことやない。当時の数学の世界は男性ばかりで、ソフィーさんも数学の研究をするには自分も男性になりすましたほうがええんやないか…と思い込んで「ルブラン」という名前の男性を装ってガウスさんと交流をもったんや

とも：ガウスの時代というと、19世紀の話か。日本では江戸時代。この時代は世界中で「女子は学問はやらんでええ」って言われてたんやな。今では考えられん話や

まゆ：実はソフィーさん、子供の頃から数学者になりたくて、当時、女性入学禁止だった学校にも男装して通ってたらしい。小学生の頃に算数帳を封印したともとは全く逆や(笑)

とも：悪かったなぁ

まゆ：話を元に戻すとソフィーさん、ガウスさんとの手紙のやりとりの中で「ソフィージェルマンの定理」を見いだすんやけど、この定理で使われる素数が「ソフィー･ジェルマン素数」やねん。ガウスさんは、これにいたく感動したらしいで(※4)

とも：また、なにやら難しそうな話になってきた

まゆ：「ソフィー・ジェルマンの定理」は「フェルマーの最終定理」を証明する過程で出てくるんやけど、それ自体は難しいものやないで

ソフィー・ジェルマンの定理
2p+1 が素数であるような素数pについて、x^p + y^p = z^p が成り立つとき、x, y, z のいずれかはpの倍数になる。

まゆ：なんでそうなるのかは、先生に聞いて

とも：だから、先生って誰やねんな(笑)

まゆ：ところで、素数にはソフィー・ジェルマン素数でもあり、安全素数でもある素数があるねん

とも：それって素数のくせに二股かけてるんか？

まゆ：その腐女子みたいな発想はやめえな(笑)。たとえば、さっき、ともが言ってた5は安全素数やけど、ソフィー・ジェルマン素数でもあるねん

とも：ということは、5がソフィー･ジェルマン素数であるためには5×2+1が素数にならんとあかんわけやなって、11は素数やん。おお！じゃあ、5は二股素数と名付けよう

まゆ：勝手に変な名前付けるな!　で、その11も安全素数でありソフィー・ジェルマン素数でもあるねん

とも：11×2+1=23…ホンマや。ひょっとして23も二股素数やろ(笑)

まゆ：そやで。でも23がソフィー･ジェルマン素数であるときの安全素数47はソフィー･ジェルマン素数ではないねんけどな。ちなみに「2, 5, 11, 23, 47」のようにソフィー･ジェルマン素数と安全素数が連続して続く数列を「カニンガム鎖」っていうねん。「カニンガム鎖」の最初と最後の数を除いた数字は、ともが言う二股素数(笑)

とも：ガム?　ちょっと、眠くなりそうやから、そこにあるガム取って?

まゆ：私、今、運転中やから、自分で手を伸ばして取りぃな！

とも：ケチやなぁ

まゆ：ケチて、別にガムは食べてええんやけど、私、運転中やん。事故起こしたら怖いやん。そうでなくても、検問で見つかったら怒られるやん

とも：あ、そっか。そうなると私の帰りが遅くなるもんなぁ。じゃあ、素数の話も終わったことやし、おとなしく寝とくわ

まゆ：あんたは、自分のことしか考えてないんかいな

とも：当たり前やん。安全運転は当然やけど、私が寝てる間に法に触れるようなこともやったらアカンで。着いたら起こしてや

まゆ：法に触れる…。あんた、まだ、私から素数の話を聞きたがってるやろ

とも：なんでやねん！

まゆ：素数には「違法素数」っていうのがあるんやけど、知っとぉ？

とも：いつものことやけど、知らん!　だいたい数字の羅列に違法とか、意味がわからん！

まゆ：まぁ興奮しいなって。2001年にアメリカでDVDのコピーソフトを作ったプログラマが著作権法違反で訴えられて「DVDコピーソフトは違法」となった裁判があってん

とも：どこに素数の話が出てくるねんな。その違法なソフトを暗号化した素数が違法素数ってこと？

まゆ：そうやないねん。この判決は当時、アメリカのソフトウェア業界で問題になって「ソフトを使って違法なコピーをしたら違法になるのはわかるけど、そのソフト自体を違法とするのは、おかしいやん」ってなってん

とも：なるほど。テレビ番組を録画して、そのソフトでDVDにコピーして、制作者に無断で売ったりしたら著作権法違反やけど、そのソフトを使って、今日のハロウィンパーティのDVDを作って友達に配るのは違法とは言えんもんなぁ

まゆ：そういうこと。その論理でいくと料理に使う包丁は人殺しもできるから、包丁は存在自体が違法ってことになる。さらにソフトウェアの場合は、元を正せば2進法という1と0の羅列やから、数字の羅列自体が違法というのもおかしいという話に発展してん

とも：2進法やったら、素数は出てこぉへんやん

まゆ：2進法は一般的にもわかりにくいしなぁ。そこで多くの人にも、この判決の問題点をわかってもらえるように、このソフトのコードを実在する素数に変換する人が現れたんや

とも：そんなことができるんや。

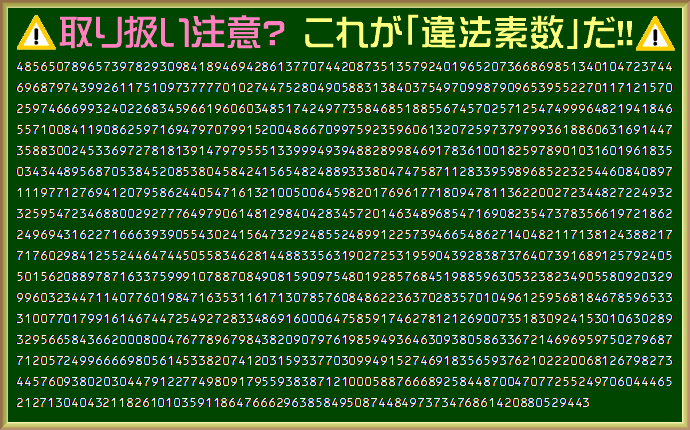
まゆ：前にも話をしたけど、アメリカのテネシー大学マーティン校のデータベースで巨大素数が登録されてるんやけど、この人は、この大学のデータベースに載っている1401桁の素数に、このソフトのコードを当てはめたんやね。つまり違法ソフトが、実在する素数と同じやった。その素数を公開することも取り締まるべきやないの…ということになってん。(※5,※6)

とも：おもしろいことを考える人がおるんやなぁ。じゃあ、その素数をメモったりしたら、アメリカでは逮捕されたりするんかな?

まゆ：アメリカではその素数をプリントしたTシャツまで売り出されたらしいけど、それを作った人や着た人で捕まったという話は聞いたことないなぁ。ちなみに私の算数帳にもメモっとぉで（笑）

とも：違法なことするなって言ったばかりやのに(笑)。 そやけど、神戸の夜景って綺麗やねぇ。宝石を散りばめたみたいで、いつ見てもうっとりするわ…って、ここどこやねん！

まゆ：ついつい素数の話が盛り上がってしもて、六甲山まで来てしもた…ごめん

♥ 脚注 ♥

※1　メドゥーサ
ギリシャ神話に登場する怪物。目を合わせると相手を石にしてしまい、髪の毛の無数のヘビで噛みつくといわれている。ともは絡み上戸で、絡む相手を睨み付け、動けなくしたところを絡んでいくという酒癖があることから、「メドゥーサ」の異名を持つ。

※2　「第6話　素数とは秘密の数である」を参照のこと。

※3　ソフィー・ジェルマン (1776〜1831)
　フランスの数学者・物理学者。裕福な家庭で育ち、少女時代に父の書斎でたまたま見つけた歴史書のアルキメデスに関する項目を読んで、数学の道を志すこととなった。しかし、当時は女性が学問をすることは社会的に認められておらず、学校も男装して通った。結局、教授に女性であることがバレてしまうが、優秀な成績であったこともあり教授の計らいで学校での勉学を続けられることが許された。ちなみに、その教授とは数学者・天文学者のラグランジュであった。
　その後も、男性を装ってガウスと手紙で交流。当時、難問とされていた「フェルマーの最終定理(予想)」に新たな考察を加えた「ソフィー・ジェルマンの定理」は、ガウスを感動させたという。
　2003年からフランス科学アカデミーでは、彼女の偉業をたたえ「ソフィー・ジェルマン賞」を創設。毎年、優秀な数学者に授与されている。

※4　ガウスがソフィー・ジェルマンが女性であることを知った出来事
　ナポレオン率いるフランス軍がヨーロッパ各地に侵略戦争を仕掛けていた1806年。ガウスがいたブラウンシュワイクにもフランス軍が侵攻。ガウスは捕虜となったが、間もなくしてフランス軍の将校から釈放が命じられ、ガウスは自由の身となった。
　その理由を将校に尋ねると「指揮官の知り合いの女性から嘆願があり、釈放することになった」とのこと。また「その女性は数学者でガウスの文通相手である」と告げられたという。ガウスは、このとき、初めて「ルブラン」という男性数学者が「ソフィー」という女性だったことに気づくこととなった。

※5　「第12話　素数とはみんなで見つける数である」を参照のこと。

※6　違法素数 (Illegal Prime)
　現在、このような意味合いをもつ素数は、本稿で取り上げた1401桁と、あるフォーマットで保存すれば、一部のコンピュータで実行可能な1811桁の素数が知られている。
→関連リンク 1401桁の違法素数：Prime Curios! 48565...29443 (1401-digits) (テネシー大学マーティン校内のサイト)
→関連リンク 1811桁の違法素数：Prime Curios! 49310...43537 (1811-digits) (テネシー大学マーティン校内のサイト)