素数とはみんなで見つける数である

まゆ：3年ぶりの史上最大の素数発見に沸く、ともの家から中継です

とも：わいてるのは、あんたの頭の中だけや。なんで、また私の家に来てるねんな！(※1)

まゆ：いつも勝手に押しかけて悪いなぁと思って、今日はお土産もってきたやん

とも：お土産って、小豆と餅米とごま塩やんかｗ　これ、どぉせえっちゅうねん

まゆ：決まってるやん。お赤飯炊くねん

とも：私、見ての通り、十分、大人やから赤飯はええねん！

まゆ：何言うとー！　巨大素数発見のお祝いやんかｗ

とも：誰が赤飯炊くねんな？

まゆ：ともに決まっとーやん

とも：勝手に決めるな。持ってくるんやったら、出来合のもの持っておいでぇな

まゆ：探してんけど、売り切れやってん

とも：まぁええわ。でも、おかずないで

まゆ：冷蔵庫にポテトサラダの残りとか、あったやん。あれでええわ。あと、缶チューハイで祝杯あげよう！

とも：人(ひと)ん家(ち)の冷蔵庫を勝手に覗くな！　いつの間に覗いてたんやｗ

まゆ：細かいことは気にせんでええでｗ

とも：気にするわ！

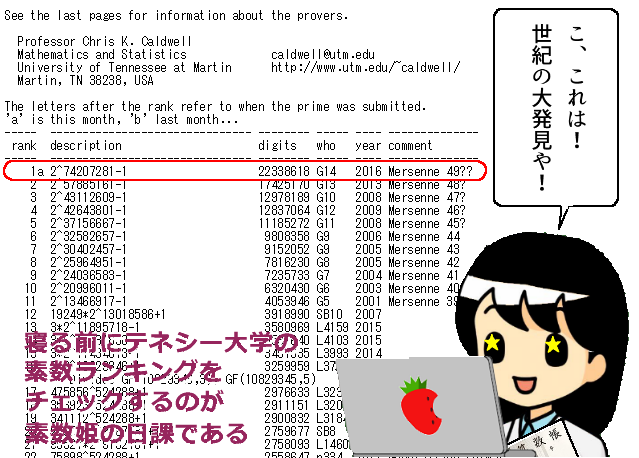
まゆ：で、今から本題やけど、今回の巨大素数はどぉやって見つけたと思う？

とも：そんなことより、まゆは、そんな情報をどこで仕入れてくるねんな。日本のマスコミでは全く報道されてないのに！(本稿発表の2016年1月20日23時現在)

まゆ：実は、これまで発見されている素数はすべてアメリカのテネシー大学マーティン校がデータベース化してるねん。知っとぉ？

とも：知らんわ！

まゆ：その大学のホームページに、上位5000位の素数のリストがあってな、毎日、寝る前、歯磨きの時に見てるねん。で、最近、代わり映えせんなぁと思ったら、昨日、1位の素数が変わっててん。興奮するやろ！

とも：あんたのほうが、よっぽど変わってるわｗ　女やったら、歯磨き中は鏡とか見ぃな

まゆ：それは大学時代に卒業した

とも：そういうもんなんか？

まゆ：昨夜は歯磨きそっちのけで、この素数の素性を調べたもんなぁ

とも：訳がわからん

まゆ：やっぱりメルセンヌ素数っぽいねん

とも：そういえば、前にメルセンヌ素数の式は巨大素数を見つけるための公式になってるって言ってたな(※2)

まゆ：よぉ覚えとーやん。そうやねん。今回発見された素数は49番目のメルセンヌ素数と言われてるねん

とも：言われてるって、どういうこと？

まゆ：45番目のメルセンヌ素数よりも大きいメルセンヌ素数は、仮のメルセンヌ素数の番号で、もしかする45番目のメルセンヌ素数と今回発見された素数の間には、未発見のメルセンヌ素数がある可能性があるねん

とも：へぇ

まゆ：へぇって、45番目のメルセンヌ素数と、今回発見された素数の差は、なんと1000万桁を超える数になるねんで。現在、観測できる全宇宙の原子の数より多いねん。何があってもおかしくないやろ。あんたの彼氏も見つかるかもしれんでｗ (※3)

とも：そんなところで見つかるとしたら、まゆの彼氏やろｗ

まゆ：今回、そんなでかい素数をどぉやって見つけたか知っとぉ？

とも：スーパーコンピュータでも使ったんか？

まゆ：それもあるかも知れんけど、個人が自宅で使うパソコンなども参加した分散コンピューティングシステムで見つかってん。実際見つけたのはアメリカのミズーリ中央大学のコンピュータなんやけどな

とも：あ、それって、宇宙人がいる星を探すみたいなやつやろ。パソコン使ってるときに、余力で調べるって言う…

まゆ：とも、そぉいうの知ってるんや。ともが言ってるのは「SETI@home」ってやつね。地球外知的生命体探査っていうねんけど、それの素数版やね

とも；そんなんがあるんや

まゆ：その中でも最も有名で、今回の素数を見つけたのが「GIMPS」(Great Internet Mersenne Prime Search)っていうプロジェクト。日本語で言えば「巨大メルセンヌ素数探査」って言えばいいのかな。上位11位までの巨大素数はこのプロジェクトから発見されてるねん ※2016年1月現在

とも：まゆはそれに参加しとんの？

まゆ：私はしてないけど、WindowsやMacOSなどの要件を満たしたパソコンがあれば誰でも参加できるねんで。専用のソフトをインストールすればあとは特に何もせんでもええねん

とも：まゆは素数好きやのに、何で参加せえへんの

まゆ；GIMPSの場合、大学などで、これ専門で動いてるコンピュータがあったりするからなぁ。個人で巨大素数を見つけるのはまず難しいわ。とはいえ、そういう個人のパソコンの余力も得て、演算してるんで、今回の素数発見の基礎になっていることには違いないけどな

とも：こういうのは他にもあるん？

まゆ：GIMPSはメルセンヌ素数を元に巨大素数を見つけるプロジェクトやけど、ほかにも「PrimeGrid」っていうプロジェクトもある。こっちのほうが「SETI@home」に似ているかな。以前は双子素数探しなどもやってたけど、今はいろんなタイプの素数で巨大素数を探してるわ。現時点で歴代51位の素数は「PrimeGrid」で見つかってんで

とも：ふーん

まゆ：素数発見プロジェクトはほかにもあるんやでぇ。日本ではあまりなじみがないけど「P.I.E.S.」(Prime Internet Eisenstein Search)はは「アイゼンシュタイン整数」という整数の定義を利用して素数を見つけるプロジェクト(※4)

とも：今、なんて言った？

まゆ：アイゼンシュタイン整数については、私もうまくは説明できひん。いや、説明できたとしても、ともには理解できんやろ(笑)。とにかく、かなり高等な整数の定義やねん

とも：あんたが知らんことを、私の責任にするな！w

まゆ：変わり種では「確率的素数」を見つけるプロジェクトっていうのもある

とも：確率的素数？何それ

まゆ：素数の可能性が高い数を見つけるっていう感じかなぁ。現時点では素数なのか、そうでないのかわからへん、検証が難しい数やね。現時点で最大の確率的素数は402万桁の数やねんけど、もし素数と認定されれば、歴代20位以内に入る素数になるかも

とも：zzzzz…

まゆ：寝てしもたわｗ　今夜も素数ランキングを眺めながら、こっそり、とものチューハイでもいただくかな

素数姫の算数帳：メルセンヌ素数にまつわるエトセトラ

♥ 脚注 ♥

※1　「番外編第5話　素数とは親友と分かち合う数である？！」を参照のこと。

※2　「第9話　素数とは完全数とともに愛すべき数である」を参照のこと。

※3　Mersenne Primes: History, Theorems and Lists

※4　「P.I.E.S.」の素数探査プログラムでは最大でも10万桁程度の素数しか探索できないが、これを発展させたものとしてフランスの数学者・Yves Gallot氏による「Cyclo」の素数探索プログラムがある。2016年1月現在、このプログラムで発見した2つの素数が巨大素数100位以内にランクインしている。