素数に恋する女：素数姫の算数帳～ゼータ関数は難しくない？

(1) ゼータ関数の基本
　「ゼータ関数」というと、とんでもなく難しい「関数」と思われがちです。これは数々の数学者がゼータ関数の数をこねくり回して、むりやり難しくしたために難解に感じるのです。ある友人に言わせると「簡単なことをむりやり難しくする数学者はマゾ」なんだそうです。
　このゼータ関数は、もともと、簡単な分数の式で表されます。数学者レオンハルト・オイラー(1707～1783)が取り組み始めたころのゼータ関数は下記のようなものでした。

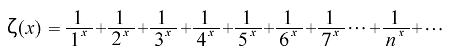
　ただ、オイラーの時代には「ゼータ関数」という言葉はなく、オイラーの論文の中では月や太陽のマークを付けて、ゼータ関数を表していたこともありました(月や太陽のマークを付けたのには諸説あるのですが、これは本編第14話を参考にしてください)。
　さて、ゼータ関数の計算方法はxにいろんな数を当てはめるのが特徴です。そして次の手順で計算を進めます。

　手順1：1,2,3,4…といった整数に対して、順番にx乗を当てはめる。
　手順2：手順1でできた数の逆数をとる。
　逆数というと難しく感じますが、例えば2のx乗の逆数は1/2^xとなります。
　手順3：手順2で作られた分数を全て合計する。

　これがゼータ関数の基本です。難しくないですよね。

(2) ゼータ関数で何がわかるの？
　では、実際に簡単なゼータ関数を計算してみましょう。
　最初の例に出したゼータ関数のxに1を当てはめてみましょう。つまり、x乗は、すべて1乗と考えます。

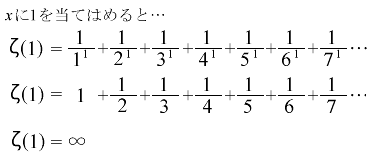
　手順3の「全て合計する」は力業になります。数は無限にあるので正直、計算ができません。しかし、この足し算、徐々に小さくなっていく分数を足し続けていきますが、その答えは無限に大きくなっていくのです。不思議ですよね。

　ではxに2を当てはめてみましょう。

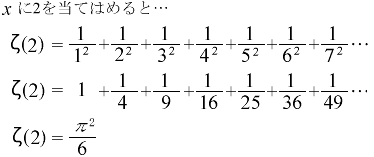
　分数を順番に見ていくと、分母の値がx=1の時よりも大きくなっています。しかし、分数のため、数としては極端に小さくなっていきます。このような数を足し続けることから、x=1の場合の答えよりも小さくなることがわかります。
　そして、この分数を足し続けると、その答えは、ある分数に限りなく近づいていくのです。
　その分数とは、円周率を2乗した数に6を割った数。これに気づいたのがオイラーでした。
　円周率となんの関係もなさそうな数の羅列なのに、順番に足していくと、なぜか円周率が関わる数の答えになっていくのです。これは2乗でなくても、他の乗数でも同じような傾向が現れます。

(3) オイラー積の発見
　この発見で、オイラーは、ゼータ関数を使って、いろいろなパターンを試します。例えば、それぞれの分数の計算に足し算や引き算を交互にして計算するとどうなるのか。そして素数だけにしたらどうなるのか。
　ここでは、のちのリーマン予想につながる「素数だけで構成されるゼータ関数」が、どうやって生まれるのかを、ざっくりと説明しましょう。

　自然数は素数と合成数に分けることができ、さらに合成数は最終的に素数に分解できます。つまり、この方法で素数だけの式を作ることができるのです。当然ながら素数だけの式でゼータ関数を計算してみても、その答えには「π」が現れるのです。
　これを「オイラー積」といいます。

(4) 音楽と関わっているゼータ関数
　オイラーは楽器を奏でる趣味を持っていました。実はゼータ関数のひらめきには、このような趣味も関わっているのではないか…とも思われるのです。
　例えば、バイオリンの音は基音と、それを1/2、1/3、1/4…の値に等しい倍音によって作られています。これらの音が組み合わさった音がバイオリンの音色なのです。古くはピタゴラスが満タンに水を張った壺をたたいたときの音。そして壺の水を1/2、1/3、1/4…と減らしたときに壺をたたいた音の違いが、それぞれ1オクターブずつ低くなっていくことを発見し、これを数学的に分析したことでも知られます。
　これらの音を数学的に表すとゼータ関数のx=1の場合と同じになります。
　ゼータ関数を計算すると円周率πに関係する数が現れますが、音楽の世界では美しい音色を表現してくれます。つまり、ゼータ関数は自然の美しさを表す数なのかも知れません。

※ゼータ関数が出てくる本編の話

♥ 第2項 < 算数帳目次 > 第4項 ♥