素数とは予想を当てる数である

まゆ：いよいよ素数界の巨匠・リーマンさんが登場や！(※1)

とも：バラエティ番組みたいなノリやなｗ

まゆ：当然、ともはリーマン、知っとぉやろ？

とも：今さら、私にそれを訊く？　まゆより詳しいで！

まゆ：お、今回は予習してきたな！

とも：あれは忘れもせぇへんで！　2008年の9月のこと。アメリカの「リーマンブラザーズ」っていう大きな証券会社が破綻したんや。この影響で為替レートが短期間に大きく動いたから、大変やってんでぇ…。ほら、私の会社、無名とはいえ商社やろ。しばらくは終電で帰ってたのを思い出すわぁ。休みの日は、疲れて、家で、ずっと寝てたからデート行く余裕もなかったもんなぁ。結局、当時つきあってた彼氏とはそれが理由で振られてしもたわ…。あー、イヤなこと思い出してしもた…(※2)

まゆ：だまらっしゃい！　予想はしてたけど、私が言うリーマンとはリーマンショックのことやないことぐらいわかるやろｗ

とも：予想できてたってことは、これぞまさしく「リーマン予想」なんちゃって。お後がよろしいようで…

まゆ：勝手に終わらせるな！ｗ　逃げようとするな！

とも：私のバッグを引っぱるな！　大人になってまで数学の難しい話はしたくないねん！

まゆ：素数の話を極めるには「リーマン予想」は避けて通られへんねん。だから、話だけでも聞いて (´・ω・`)

とも：そんなことで、泣きそうな顔をせんといて。私が悪いみたいやんｗ　話を聞くだけやで。この前みたいに、1兆までの素数の数を計算したりせぇへんで！

まゆ：じゃあ、「π(x)」って知っとぉ？

とも：立ち直り早いなｗ　円周率とか出てきたら、私が泣くで

まゆ：このπって、円周率のことやないねん。日本語で言えば「素数計数関数」っていうねん

とも：円周率と関係ないのに、なんでπが出てくるんや

まゆ：素数計数関数(prime-counting function)のギリシャ語の頭文字の「π」から取ったらしいわ。紛らわしかったらπの代わりに「とも(x)」に置き換えてもええねんで……って…あんた、ないなぁ

とも：パイがなくて悪かったなぁ！帰るで！

まゆ：ごめんごめん。「π(x)」には前回のあの話が集約されてるねん

とも：あの階段から始まって1兆までの素数を数える話って、たった4文字の関数で済むんかいｗ

まゆ：そゆこと

とも：あれだけ話を膨らませた私の苦労は、なんやったんやｗ

まゆ：「π(x)」のxに「100」を入れると「25」の答えが出てくる。つまりxまでの素数を数えるための関数やねん。簡単やろ

とも：確かに、高校で数学が選択科目になったとき、数学を取らなかった私にも理解できるわ

まゆ：数式とか、関数は全然、難しくないねん。見慣れない文字があるから難しく見えるだけやねん。これを踏まえて、今日の話で出てくるのが「ζ(s)」や

とも：何これ？

まゆ：ゼータ関数っていうねん。簡単そうやろｗ

とも：見た目は簡単そうやなぁ

まゆ：せやろｗ　これはこんな式になるねん

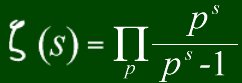
とも：ちょっと待った！何これ。こんなん見せられたら、じんましん出るわ！(※3)

まゆ：じんましんにええ薬があるから、もう少し、私の話を聞いて

とも：ここで、おもむろに薬のカタログを取り出すなｗ

まゆ：難しそうやけど、簡単にするとこんな感じ。素数の入った分数を永遠に掛けていくだけやねん

とも：s乗とか、見慣れんのが出てくるけど…

まゆ：「s」は「変数」といって「ここに、いろんな数を当てはめるで」っていう意味ね。一般的におなじみの「x」でも良かってんけど、リーマンさんが「s」を使ってたんで、ここでも「s」とするわ

とも：リーマンってSなんかｗ　数学者って、むりやり物事を難しく考えてるからMか思ったんやけど…(※4)

まゆ：あんたなぁ、最近、数学者の間で、このサイトが話題になっとーみたいやから、言葉に気ぃつけや

とも：まじで！？　じゃ、じゃあ…話を戻すわ。今まで説明を聞いてきたけど、わかったような、わからんような…

まゆ：理解せんでもええｗ　「素数が入ってる分数の式がある」っていうのを感じるだけでええわｗ　私もこれを説明せぇって言われると困るｗ

とも：わかった！感じるわｗ

まゆ：感じてもらったところで、この式が、リーマン予想の真骨頂やねん

とも：ただでさえ難しい話やのに、難しい言葉使いなｗ　烏骨鶏(うこっけい)って(※5)

まゆ：文系のあんたに無理してあわせたんやけど…烏骨鶏とは言ってないでｗ　つまり、リーマン予想の姿

とも：なるほど！　で、この式で何が予想できるの？来週のロトくじの当選番号とか？

まゆ：そんなん、わかるわけないやんｗ　素数って規則性がないやろ。でもこの数式をグラフ化すると不思議なことが起こるねん

とも：不思議なことって、ここで、私のモテ期を奪ったリーマンショックの悪夢が蘇るんか！？(※2)

まゆ：なんでリーマンショックが出てくるねんｗ　でも数学界に衝撃を与えたのは間違いないけどな　分数にある素数をs乗しただけの式やのに、グラフにすると、ある規則性がはっきりと出てくるねん

とも：はっきりと出てくるって、なんか、ワクワクするな！　ガウスの素数定理の時は「何となく」…っていうイメージやったからなぁ

まゆ：「ゼータ関数の非自明なゼロ点は、すべて実部の1/2の一直線上にあるはずや！」

とも：な、何、言うとー？

まゆ：ざっくり言うと、この式の「s」にいろんな数を入れて、グラフにしたときに、グラフの高さが「0」になる非自明な点が、実数軸の1/2の線上に並ぶねん。ここではあえて「高さ」って言うけど、ホンマはこれ「四次元」のグラフになるんで高低差で説明するのは正しくはないんやけどな

とも：四次元って、ドラえもんのポケットの世界なんか？

まゆ：そーいうのとは違うでｗ　興味があれば「解析学」っていうのを勉強すればええわ。「リーマン予想のゼロ点」を厳密に理解するには「解析接続」とか…

とも：あんたの言うとーことが異次元で理解不能やわ。話を進めてｗ

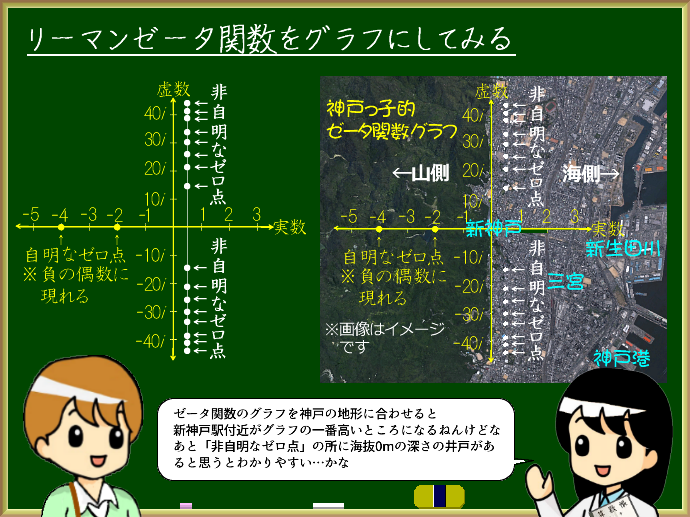
まゆ：その四次元であるリーマン予想のグラフを三次元化。しかも神戸の地形に無理矢理当てはめてみた。わかりやすいやろｗ　高低差でいうと新神戸駅辺りが一番高い所になるねんけど

とも：私はええけど、その例え方は、数学の先生方には怒られんのかｗ

まゆ：研究者の中には、ケーキにしとー人もおるねんで

とも：数学者って、やっぱり変…

まゆ：こら！数学者を敵に回すな！　今回の話でも、裏では、数学者の方に、ずいぶんお世話になってたりするから

とも：わかった

まゆ：新神戸駅前の、あの高層ホテルがグラフの高い点。布引の滝とか布引貯水池は自明なゼロ点、野崎通山麓線や異人館通あたりが実数部の1/2の線。非自明なゼロ点は、その道路に海抜0mの深さの井戸があるようなイメージかなｗ

とも：その例え、神戸の人しかわからんわｗ　ところで「非自明」って何？

まゆ：「自明でない」ってことやん

とも：ごめん、質問の仕方が悪かったわｗ　じゃあ「自明」って何？

まゆ：自明っていうのは「そこにあって当然」って言う感じかな。ちなみにゼータ関数で「自明なゼロ点」はマイナスの偶数のところに並ぶねん

とも：つまり「非自明なゼロ点」は「どこにあるかわからないゼロ点」ってことかな。で、その点がなぜか実数の「1/2」の線に並ぶ…っと

まゆ：あんた、わかっとーやん！　さすがやｗ

とも：それで、素数と、どーつながるねんな

まゆ：これまで、ともは散々、素数に規則性がないとか(※6)、素数は肝心なところで期待を裏切るとか(※4)、まゆは可愛いとか言ってきたけど…

とも：私が言ったこともないセリフが混ざっとーでｗ

まゆ：つまり「ゼータ関数の非自明なゼロ点は、すべて実数部の1/2の一直線上にあるはずや！」イコール「素数に何らかの規則性があるはずや！」ってことやねん。これが「リーマン予想」の正体

とも：まとめると、ゼータ関数と呼ばれる素数だけでできた分数の式をグラフにすると、グラフの高さが0になる点が一直線に並ぶところがある。つまり、素数に何らかの規則性があるからや…ってことやね

まゆ：おお！文系！まとめるのうまいな！　そういうこと。でも、これを見つけたリーマンは、この規則性を証明しようとはしなかってん

とも：予想するだけして、ほったらかしなんかい！ｗ

まゆ：なぜかというと、リーマンは素数でできた分数の式をグラフ化したときの「非自明なゼロ点」が一直線に並ぶ理由よりも、素数そのものを見つける方法を探したかってん

とも：確かに、これでは素数に規則性があるらしい…ということはわかっても、ズバリ素数を見つけるのは難しそうやなぁ

まゆ：リーマン自身も「リーマン予想は素数探しの副産物」と考えていたようで、「この予想は自分の研究目標からすると不必要」とまで言ったそうな

とも：数学嫌いの私ですら「リーマン予想」と言えば、数学界で最も難しい未解決問題って知っとーのに、当の本人は軽く考えてたんやなぁｗ

まゆ：コンピュータが発達した現在ですら、証明されていない大問題やのにねぇ。しかも証明したら100万ドルの懸賞金がもらえるんやで(※7)。それに、リーマン予想を証明しようとして精神病になって病院送りになった数学者もいるし(※8)

とも：リーマン、恐ろしいな。私もモテ期をつぶされて、未だに独身やからなぁ(※2)

まゆ：相当、根に持ってるなｗ　ここで、また素数階段の話に戻すわｗ

とも：私もいやな思い出なんで、素数階段の話につきあうわｗ　前回、ガウスは自分が編み出した素数定理で素数階段を再現できんかったっていう話やね

まゆ：うん。そう。リーマンはリーマン予想よりも、ガウスの素数階段の修正を考えてたんや

とも：一直線に並ぶゼロ点よりも、ズバリ素数を見つけたいもんなぁ

まゆ：リーマンは「ガウス師匠は、あともぉちょっとやったのに！」という前提で、それを元に補正する式を思いついたんや

とも：師匠思いのええ弟子やなぁ。リーマン

まゆ：リーマンが編み出した関数が「π(x)〜R(x)」。簡単やろｗ

とも：その言葉には騙されんで！　その後にめっちゃ難しい式が隠れとぉんやろ

まゆ：バレたｗ　じんましんに効く薬、ここに置いとくわ

とも：xまでの素数の数は正確にわかるようになったけど、これでは、どの数が素数なのかまでは、わからんの違う？

まゆ：うん。xを1つずつ、ずらして計測すれば、その答えが1つ上がったところで、xが素数ってわかるんやけど、結局、1から数を数えて、素数を判定していることと変わらんからなぁ…

とも：ところで、よく「リーマン予想」が証明されると、この前、話していた暗号化通信が簡単に解読されるっていうけど、ホンマ？(※9)

まゆ：それはないわ。証明はされてないだけで、「リーマン予想」は結果として、非自明なゼロ点が永遠と実数部の1/2の上に並んでいるんで、解読されるとしたら、すでに解読されてるはず。解読されていないということは、リーマン予想が証明されても、暗号化通信には影響はほとんどない…と言えるんじゃないかな

とも：なるほどなぁ…　あと、もう1個、質問してもええ？

まゆ：何？　難しい質問はやめてや。細かいところは私も説明できんｗ

とも：めっちゃ簡単。「1+1の答えは？」よりも簡単。このホームページの「このウェブサイトについて」のところで「『リーマン予想』『ルジャンドル予想』など難しい話は取り上げません」って書いてあるんやけど、今日の話のテーマってなんやったっけ？(※10)

まゆ：えっ？　な、なんやろなぁ？　強いていうなら…「リーマンショックによる1人の女の悲恋の物語」…みたいな？(※2)

とも：いやなこと、思い出させるな！　リーマン、許さんからなぁ！

素数姫の算数帳：ゼータ関数は難しくない！

♥ 脚注 ♥

※1　ベルンハルト・リーマン (1826〜1866)
　ドイツの数学者。ガウスの弟子でもある。高校の数学で習う積分は正確には「リーマン積分」といい、リーマンが考案したものである。素数界ではリーマンゼータ関数から導きだされた「リーマン予想」で知られるが、幾何学、解析学でも業績を上げた。
　持病の結核が悪化して39歳でこの世を去るが、リーマンが論文作成で残した数式のメモなど資料の多くは、死後、家政婦によって破棄された。そのため、未だに、論文には未解明な部分が多く残されている。

※2　リーマンショック
　2008年9月、アメリカの住宅ローンの不良債権化で、多額の不良債権を抱えた投資銀行「リーマンブラザーズ」が経営破綻したことをきっかけに始まった世界的金融不安。
　日本にもその影響が直撃、為替レートは2008年9月には1ドル106円台だったが、リーマンブラザーズ破綻直後は1ドル90円台に推移。急激な円高となった。日経平均株価も2ヶ月間で6000円以上も下落した。
　とも曰く「あれさえなければ、今頃、幸せな生活を送ってたはずや。ここで素数の話なんかしてない！」

※3　じんましん
　皮膚の一時的なアレルギー反応。一般的には食べ物によるじんましんが知られるが、入浴後のかゆみや、薬の服用による軽いかゆみなどもじんましんの一種である。まれにストレスからじんましんを発疹する人もおり、数式をみてじんましんになる人もいないとは言い切れない。が、ともは食べ物の好き嫌いはなく、ストレスもため込まない性格なので、この手の病気とは無縁である。

※4　「第6話　素数とは家族の数である」を参照のこと。

※5　烏骨鶏
　ニワトリの一種。外見は白い綿毛のような羽毛で覆われているが、皮膚や内臓、そして骨まで黒いという特徴がある。中国では食べると不老不死になると言い伝えられる。

※6　ともも言っていることもあるが、どちらかと言えば、まゆがよく言っている

※7　数学の未解決問題にかけられた懸賞金
　アメリカのクレイ数学研究所は数学界の未解決問題を証明した人に対して100万ドルの懸賞金を支払うことを表明している。2010年、「ポアンカレ予想」を証明したロシアの数学者ペレルマンに対して懸賞金が支払われる予定だったが、ペレルマンは「数学界の不公平さ」を理由に賞金の受け取りを拒否している。なお、検証には数年を要すため、即座に支払われるわけではない。ポアンカレ予想の時は証明発表から7年後に懸賞金の支払いが決定した。

※8　ジョン・ナッシュ (1928〜2015)
　アメリカの数学者。ノーベル経済学賞受賞者。
　1950年代、リーマン予想の証明にこだわるあまり、統合失調症となったといわれ、1961年から約9年間、精神病院に入院した。退院後も通院と投薬治療を続けるが、その後、治療を拒否した。
　彼の生涯は存命中の2001年に「ビューティフルマインド」というタイトルで映画化されるが、その際、精神病の投薬治療を中断することはないようにシナリオを書き換えさせたといわれる。これは自分と同じ病気をもつ患者へ悪影響をもたらさないための配慮とされる。
　彼以外にも、リーマン予想に関わり、体調や精神に変調をうったえる数学者が相次いだため、1960年代、数学者の間でリーマン予想に関わることを敬遠する動きがあった。

※9　「第6話　素数とは秘密の数である」を参照のこと。

※10　当サイトの「このウェブサイトについて」にリーマン予想は取り上げない旨が記載されていた。現在は証拠隠滅が謀られているが、証拠保全のため、本稿が掲載された翌日(2016年1月25日)の画面ショットが残されている。